B5 – Effiziente Simulation und Modellreduktion für Offshore-Windenergieanlagen (beendet 2024)

Die Simulation von mechanischen Megastrukturen wie Offshore-Windkraftanlagen ist rechenintensiv. Um in der ersten Förderperiode einen Beitrag zur Entwicklung eines robusten und effizienten, nahezu echtzeitfähigen digitalen Zwillings zu leisten, verfolgte das TP B05 zwei Ziele. Das erste Ziel war die Anwendung der Hauptgeodätenanalyse (principal component analysis - PGA) als strukturerhaltende Modellreduktion (MOR) für die direktorbasierte Dynamik des Struktur-Teils des digitalen Zwillings (DeSiO). Das zweite Ziel war die Verbesserung der nichtlinearen und linearen Löser des impliziten Zeitschritts für den mechanischen Teil, insbesondere die Entwicklung robuster und effizienter direkter und iterativer Algorithmen für das dünnbesetzte Sattelpunktsystem und eines inexakten Newton-Algorithmus, der die Genauigkeit des iterativen linearen Lösers adaptiv steuert.

Hauptgeodätenanalyse (PGA)

Basierend auf unserer früheren Studie zu PGA [1], untersuchen wir PGA im Bezug auf die nichtlineare Dynamik von Balkenstrukturen und befassen uns dabei mit mehreren neuen Herausforderungen.

Für dynamische Simulationen haben wir Lifts für langfristige periodische Bewegungsdaten konstruiert, die Zweigwechsel des Riemannschen Logarithmus erfordern. Diese Wechsel treten in Singularitäten in den Logarithmen von SO(3) (Rotationsgruppe) und S² (Einheitssphäre) auf, was Probleme aufwirft, die in der bisherigen Literatur nicht behandelt wurden [2] [3] [4] [5].

Wir entwickelten präzise mathematische Formulierungen für nichtlineare Abbildungen, Projektionen auf SO(3) und S² sowie Zweig-wechselde-Algorithmen, die alle in C++ implementiert wurden. Wir analysierten die numerische Genauigkeit dieser Karten anhand von Millionen von Snapshots, die aus DeSiO-Simulationen mechanischer Systeme, z. B. einem diskretisierten Windturbinenmodell, gewonnen wurden, mit variierender Genauigkeit. Die vollständigen Ergebnisse sind in Gebhardt et al. (2023) aufgeführt.

Um die Genauigkeit zu verbessern, haben wir unsere C++-Implementierungen von PGA-bezogenen nichtlinearen Abbildungen für S² mit prozessor- und compilerspezifischen Techniken optimiert (Schubert & Steinbach, 2023). Dabei wurde eine eingebaute Normberechnungsfunktion mit leichten Ungenauigkeiten und ein möglicher GCC-Compilerfehler aufgedeckt, der die Genauigkeit der Division beeinträchtigt.

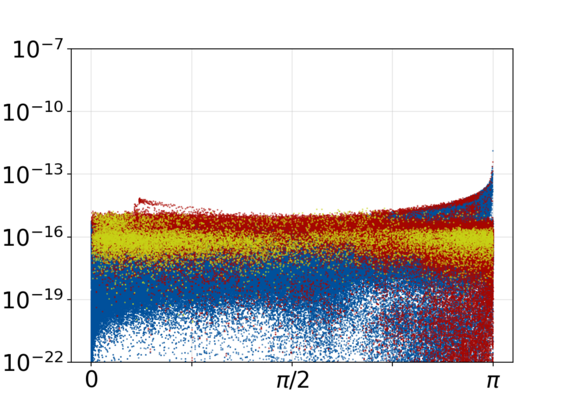
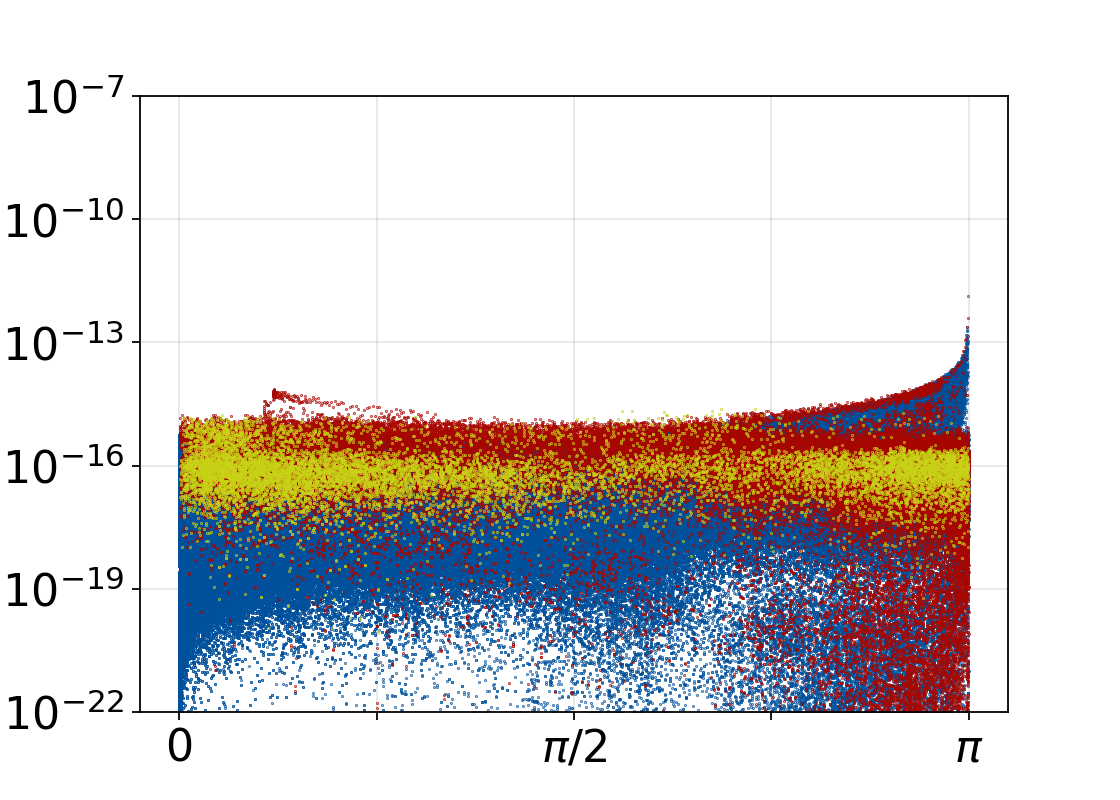
Zusammenfassend lässt sich sagen, dass der PGA-Ansatz schlechte Energieerhaltungseigenschaften aufweist, während er eine moderate Verringerung der Systemdimension ermöglicht. Da eine vollständige PGA-basierte Simulation mit reduzierter Ordnung zusätzlich zwei Koordinatentransformationen und eine Lösung eines nichtlinearen Kleinste-Quadrate-Problems pro Zeitschritt erfordern würde [1], kommen wir zu dem Schluss, dass der Ansatz für die strukturerhaltende Reduzierung der Modellordnung in unserer Anwendung nicht vielversprechend ist. Der von uns entwickelte PGA-Code ist jedoch für die Bewegungsanalyse und wahrscheinlich auch für viele andere Zwecke gut geeignet.

Inexakter Newton Löser

Unser Ziel war es, eine inexakte Newton-Methode für das Sattelpunktproblem in DeSiO zu entwickeln, wobei wir maßgeschneiderte dünn besetzte direkte und iterative Löser verwendeten. Die Integration der aero-elastischen Wind-Rotor-Kopplung über die instationäre Wirbelgitter-Methode (UVLM) führte dichte aerodynamische Blöcke in die Strukturmatrix ein und störte deren nahezu symmetrische und dünnbesetzte Struktur. Die Lösung des gesamten Systems war sehr rechenaufwändig, und ein vereinfachter Ansatz schlug manchmal fehl.

Um dieses Problem zu lösen, haben wir einen inexakten Newton-Algorithmus entwickelt. Der in C++ implementierte Algorithmus wurde in DeSiO an zwei Problemen des Teilprojekts Z01 getestet, wobei exakte Newton-, Quasi-Newton- und ungenaue Newton-Methoden verglichen wurden (Schubert et al., 2024).

Diese Methoden bieten erhebliche Geschwindigkeitssteigerungen, haben aber nur begrenzte Auswirkungen auf die Gesamtsimulationszeiten, da die Lösung linearer Systeme nur etwa 4 bis 6 % des Simulationsaufwands ausmacht. Die meiste Rechenzeit wird für die Auswertung der aerodynamischen Kräfte und Ableitungen mit der UVLM aufgewendet. Die inexakte Newton-Methode reduziert den Aufwand für den Wind nur geringfügig.

Zusammenfassend lässt sich sagen, dass der Ersatz von Pardiso durch einen benutzerdefinierten linearen Sattelpunktlöser für rein mechanische Systeme vorteilhaft, für aeroelastische Simulationen, bei denen UVLM-Auswertungen dominieren, jedoch unpraktisch ist. Während unser geplanter inexakter Newton Löser die Leistung im aeroelastischen Rahmen verbessert, sind die Gewinne durch die Kosten der Ableitungsberechnungen begrenzt.

Andere Zusammenarbeit im SFB

Wir haben mit dem TP C04 zusammengearbeitet, um kleine Schadensfälle in flexiblen mechanischen Strukturen auf der Grundlage von Schwingungsmessungen zu ermitteln, was zu einem nicht-glatten und nicht-linearen bi-objektiven Parameterschätzungsproblem führt. Wir arbeiteten an der mathematischen Formulierung dieses Optimierungsproblems und an einem multikriteriellen globalen Mustersuchalgorithmus mit einem speziellen nicht-dominierten Sortierverfahren zur Berechnung von Pareto-Fronten (Günther et al., 202X).