B5 - Efficient simulation and model reduction for offshore wind turbines (endet 2024)

The simulation of mechanical megastructures like offshore wind turbines is computationally highly expensive. In order to contribute to the development of a robust and efficient, nearly real-time capable digital twin in the first funding period, the objectives of SP B05 were twofold. The first goal was to apply principal geodesic analysis (PGA) as a structure-preserving model order reduction (MOR) technique for the director-based dynamics of the mechanical part of the digital twin (DeSiO). The second goal was to improve the nonlinear and linear solvers of the implicit time step for the mechanical part, in particular to develop robust and efficient direct and iterative algorithms for the sparse saddle-point system and an inexact Newton algorithm which adaptively controls the accuracy of the iterative linear solver.

Principal Geodesic Analysis

Based on our previous study on PGA [1] we investigated PGA for analysing the nonlinear dynamics of beam structures and addressed several novel challenges.

For dynamic simulations, we constructed lifts for long-term periodic motion data, requiring branch-switching in Riemannian logarithm maps. These switches occur at singularities in the SO(3) (rotation group) and S² (unit sphere) logarithm maps, posing problems unaddressed in prior literature [2] [3] [4] [5].

We developed precise mathematical formulations for nonlinear maps, projections to SO(3) and S², and branch-switching algorithms, all implemented in C++. Computationally, we analyzed the numerical accuracy of these maps using millions of snapshots generated from DeSiO simulations of mechanical systems, such as a discretized wind turbine model, with varying accuracy. Full results are detailed in Gebhardt et al. (2023).

To improve accuracy, we optimized our C++ implementations of PGA-related nonlinear maps for S² using processor- and compiler-specific techniques (Schubert & Steinbach, 2023). This revealed a built-in norm computation function with slight inaccuracies and a possible GCC compiler bug affecting division precision

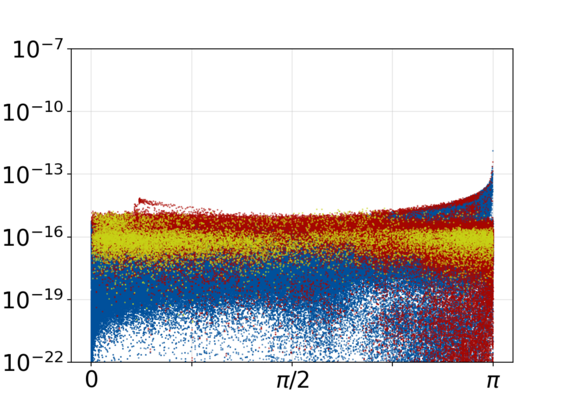
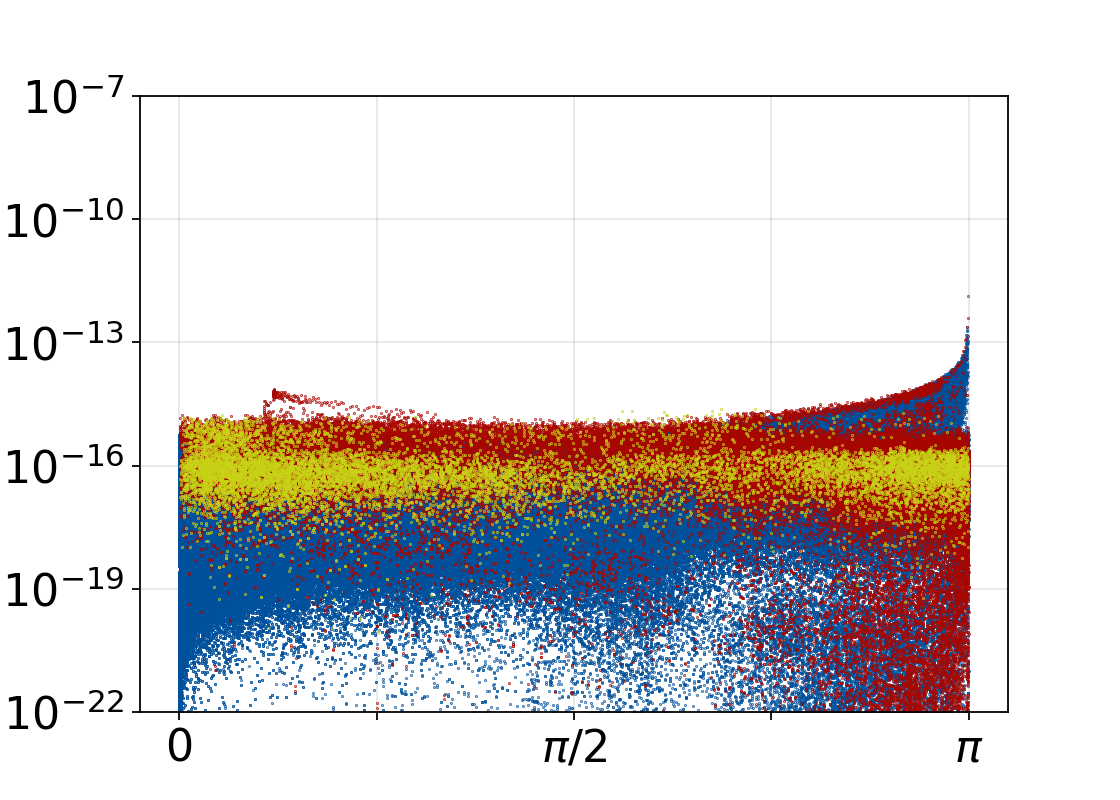
In summary, the PGA approach shows poor energy conservation properties while allowing moderate reductions of the system dimension. Since a complete PGA-based reduced-order simulation would additionally require two coordinate transformations and one solution of a nonlinear least-squares problem per time step [1], we conclude that the approach is not promising for structure-preserving model order reduction in our application. However, the PGA machinery that we have developed is well suited for motion analysis and probably many other purposes.

Inexact Newton Solver

We aimed to develop an inexact Newton method for the saddle-point problem in DeSiO, using custom sparse direct and iterative solvers. The integration of aero-elastic wind-rotor coupling via the unsteady vortex-lattice method (UVLM) introduced dense aerodynamic blocks into the structural matrix, disrupting its near-symmetric and sparse structure. Solving the full system was computationally costly, and a simplified approach sometimes failed.

To address this, we designed an inexact Newton algorithm. Implemented in C++, the algorithm was tested in DeSiO on two problems from subproject Z01, comparing exact Newton, quasi-Newton, and inexact Newton methods (Schubert et al., 2024).

These methods offer significant speed-ups but have limited impact on total simulation times, as solving linear systems only accounts for about 4% to 6% of the simulation effort. Most computational time is spent evaluating aerodynamic forces and derivatives using the UVLM. The inexact Newton method only modestly reduces effort for the wind turbine model due to convergence control requiring expensive aerodynamic derivatives.

In summary, replacing Pardiso with a custom linear saddle-point solver is beneficial for purely mechanical systems but impractical for aeroelastic simulations where UVLM evaluations dominate. While our planned inexact Newton development improved performance in aeroelastic settings, gains are limited by the cost of derivative computations.

Other Collaborations within the CRC

We worked together with SP C04 to pinpoint small instances of damage in flexible mechanical structures based on vibration measurements, which leads to a nonsmooth and nonlinear bi-objective parameter estimation problem. We worked on the mathematical formulation of this optimisation problem and on a multi-objective global pattern search algorithm with a specialised non-dominated sorting procedure for computing Pareto fronts (Günther et al., 202X).